Mesh Analysis Using Matrix Form

Mesh Analysis Using Matrix Form

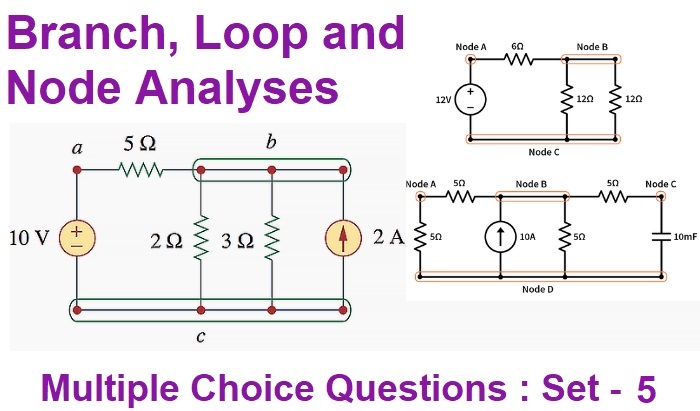
Consider the network of Figure given below, which contains resistances and independent voltage sources and has three meshes. Let the three mesh currents be designated as I₁, I₂ and I₃ and all the three may be assumed to flow in the clockwise direction for obtaining symmetry in mesh equations.

Applying Kirchhoff’s Voltage Law to mesh (i), we have

E₁ − I₁R₁ − R₃ (I₁ − I₃) − R₂ (I₁ − I₂) = 0

(R₁ + R₂ + R₃) I₁ − R₂I₂ − R₃I₃ = E₁ ………………………..(i)

Similarly, from mesh (ii), we have

E₂ − R₂ (I₂ − I₁) − R₅ (I₂ − I₃) − I₂R₄ = 0

− R₂I₁ + (R₂ + R₄ + R₅) I₂ − R₅I₃ = E₂ ………………………..(ii)

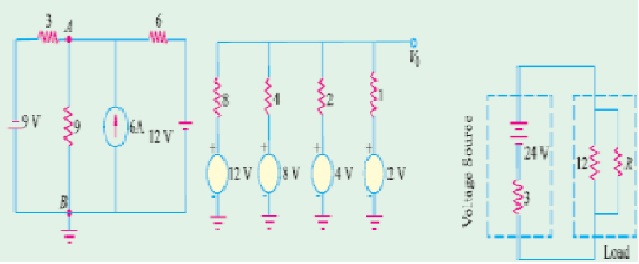
Applying Kirchhoff’s Voltage Law to mesh (iii), we have

E₃ − I₃R₇ − R₅ (I₃ − I₂) − R₃ (I₃ − I₁) − I₃ R₆ = 0

or − R₃I₁ − R₅I₂ + (R₃ + R₅ + R₆ + R₇) I₃ = E₃ ………………………(iii)

It should be noted that signs of different items in the above three equations have been so changed as to make the items containing self resistances positive (please see further).

The matrix equivalent of the above three equations is

It would be seen that the first item is the first row i.e. (R1 + R2 + R3) represents the self resistance of mesh (i) which equals the sum of all resistance in mesh (i). Similarly, the second item in the first row represents the mutual resistance between meshes (i) and (ii) i.e. the sum of the resistances common to mesh (i) and (ii). Similarly, the third item in the first row represents the mutual-resistance of the mesh (i) and mesh (ii).

The item E1, in general, represents the algebraic sum of the voltages of all the voltage sources acting around mesh (i). Similar is the case with E2 and E3. The sign of the e.m.f’s is the same as discussed in Article Determination of voltage sign i.e. while going along the current, if we pass from negative to the positive terminal of a battery, then its e.m.f. is taken positive. If it is the other way around, then battery e.m.f. is taken negative.

In general, let

R11 = self-resistance of mesh (i)
R22 = self-resistance of mesh (ii) i.e. sum of all resistances in mesh (ii)
R33 = Self-resistance of mesh (iii) i.e. sum of all resistances in mesh (iii)
R12 = R21 = − [Sum of all the resistances common to meshes (i) and (ii)]
R23 = R32 = − [Sum of all the resistances common to meshes (ii) and (iii)

R31 = R13 = − [Sum of all the resistances common to meshes (i) and (iii)]
Using these symbols, the generalized form of the above matrix equivalent can be written as

If there are m independent meshes in any liner network, then the mesh equations can be written in the matrix form as under :

The above equations can be written in a more compact form as [R_m] [I_m] = [E_m]. It is known as Ohm’s law in matrix form.

In the end, it may be pointed out that the directions of mesh currents can be selected arbitrarily. If we assume each mesh current to flow in the clockwise direction, then

(i) All self-resistances will always be positive and

(ii) all mutual resistances will always be negative. We will adapt this sign convention in the solved examples to follow.

The above main advantage of the generalized form of all mesh equations is that they can be easily remembered because of their symmetry. Moreover, for any given network, these can be written by inspection and then solved by the use of determinants. It eliminates the tedium of deriving simultaneous equations.

Read article – Determination of voltage sign

Visit NCERTplanet.com for NCERT solutions and Textbook downloads